


Next: Discussion
Up: Testing for non-linearities
Previous: Testing a non-linearity correction
Measurement of non-linearity using the ratio method
The ratio method can be used to determine a non-linearity curve, for
example, by solving an equation of the form
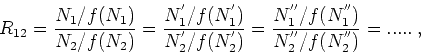 |
(2) |
where  and
and  are the measured counts of the two regions, at
different light levels
are the measured counts of the two regions, at
different light levels 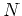

 etc.,
etc., 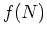 is the
non-linearity function equivalent to measured-counts / expected-counts
and,
is the
non-linearity function equivalent to measured-counts / expected-counts
and,  is the ratio of the expected (or true) counts between
the two regions (the corrected ratio). A fit can be made to the
parameters chosen for the non-linearity function, by minimising the
scatter in the corrected ratio between different light levels.
Similar equations can be solved for different pairs of regions on the
CCD. For low intensity non-linearity tests, it will be necessary to
obtain a good over-scan region for accurate bias subtraction.
is the ratio of the expected (or true) counts between
the two regions (the corrected ratio). A fit can be made to the
parameters chosen for the non-linearity function, by minimising the
scatter in the corrected ratio between different light levels.
Similar equations can be solved for different pairs of regions on the
CCD. For low intensity non-linearity tests, it will be necessary to
obtain a good over-scan region for accurate bias subtraction.
In 1998 December, we observed at Mt. Stromlo using
CCD17
(2Kx4K SITe with a nominal gain of 2.5e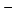 /ADU and 1x2 binning).
We measured the non-linearity of this CCD using the ratio method.
/ADU and 1x2 binning).
We measured the non-linearity of this CCD using the ratio method.
Barton (1986) described the AAO CCD non-linearities in terms of an
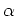 parameter (see also Gilliland et al. 1993, Leach et al.
1980 and Tinney 1996),
similar to
parameter (see also Gilliland et al. 1993, Leach et al.
1980 and Tinney 1996),
similar to 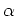 in the equation:
in the equation:
 |
(3) |
where 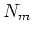 are the measured counts in ADU above the bias level and
are the measured counts in ADU above the bias level and
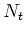 are the `true counts' (normalised so that
are the `true counts' (normalised so that  for
for
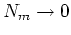 ). The non-linearity of CCD17 was assumed to be
represented by this single parameter. For high sensitivity to this
parameter when using the ratio method,
). The non-linearity of CCD17 was assumed to be
represented by this single parameter. For high sensitivity to this
parameter when using the ratio method,  should be in the range
0.15-0.45.
should be in the range
0.15-0.45.
For each set of ratio measurements, 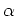 was varied until the best
fit for the corrected ratios had a slope of zero. The fit was
obtained using the ratios with counts of the higher-value between 0
and 40000. Lower weight was given to those with counts below
10000 because of increased noise.
Figures 6-8 show the value of
was varied until the best
fit for the corrected ratios had a slope of zero. The fit was
obtained using the ratios with counts of the higher-value between 0
and 40000. Lower weight was given to those with counts below
10000 because of increased noise.
Figures 6-8 show the value of 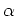 and the corrected ratios, for three sets of measurements. For CCD17,
and the corrected ratios, for three sets of measurements. For CCD17,
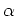 is about
is about
 .
.
Figure 6:
Non-linearity measurement of CCD17 using ratio method. The squares
represent the measured ratios, while the asterisks represent the
ratios after correcting the intensities using the alpha parameter
[
 ]. The lines are best fits to each
set of ratios, between 0 and 40000 counts, with lower weight given
to measurements below 10000. The alpha value has been chosen so
that the slope of the best fit to the corrected ratios is zero.
]. The lines are best fits to each
set of ratios, between 0 and 40000 counts, with lower weight given
to measurements below 10000. The alpha value has been chosen so
that the slope of the best fit to the corrected ratios is zero.
 |
Figure 7:
Non-linearity measurement of CCD17. See Fig. 6 for
details.
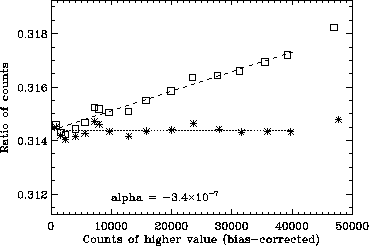 |
Figure 8:
Non-linearity measurement of CCD17. See Fig. 6 for
details.
 |
The ratio method removes the problems of requiring accurate exposure
times and lamp-temperature stability to make accurate non-linearity
measurements. Improvement of the accuracy of the method described in
this section could be made by
(i) taking more exposures,
(ii) increasing and decreasing the exposure time several times, and
(iii) interspersing the exposures with bias frames.
In the second case, this will reduce problems which might arise from a
systematic change in the measurements with time. In the third case,
monitoring any changes in bias frames will improve the accuracy of
bias subtraction which is critical for measurements with low counts.



Next: Discussion
Up: Testing for non-linearities
Previous: Testing a non-linearity correction
Ivan Baldry
2005-05-23
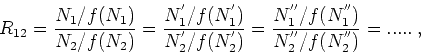
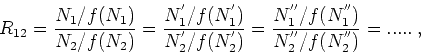
![]() /ADU and 1x2 binning).
We measured the non-linearity of this CCD using the ratio method.
/ADU and 1x2 binning).
We measured the non-linearity of this CCD using the ratio method.
![]() parameter (see also Gilliland et al. 1993, Leach et al.
1980 and Tinney 1996),
similar to
parameter (see also Gilliland et al. 1993, Leach et al.
1980 and Tinney 1996),
similar to ![]() in the equation:
in the equation:
![]() was varied until the best
fit for the corrected ratios had a slope of zero. The fit was
obtained using the ratios with counts of the higher-value between 0
and 40000. Lower weight was given to those with counts below
10000 because of increased noise.
Figures 6-8 show the value of
was varied until the best
fit for the corrected ratios had a slope of zero. The fit was
obtained using the ratios with counts of the higher-value between 0
and 40000. Lower weight was given to those with counts below
10000 because of increased noise.
Figures 6-8 show the value of ![]() and the corrected ratios, for three sets of measurements. For CCD17,
and the corrected ratios, for three sets of measurements. For CCD17,
![]() is about
is about
![]() .
.
