


Next: Bibliography
Resolving Powers of Immersed Transmission Gratings
I. K. Baldry, J. Bland-Hawthorn & J. G. Robertson
Appendix of Publ.
Astron. Soc. Pacific, Vol. 116, pp. 403-414;
published in May 2004.
Keywords: spectral resolution diffraction grating prism
VPH gratings can be sandwiched between glass prisms. This reduces the total
beam deviation and reduces the air-to-glass incidence angle (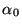 ), for
a given grating and wavelength. This can be useful because the total beam
deviation is limited by the physical sizes of the camera and collimator and
because higher incidence angles on air-glass boundaries give higher reflection
losses (for unpolarized light). Here, we give the equations for calculating
the resolving power of a transmission grating immersed between two prisms.
), for
a given grating and wavelength. This can be useful because the total beam
deviation is limited by the physical sizes of the camera and collimator and
because higher incidence angles on air-glass boundaries give higher reflection
losses (for unpolarized light). Here, we give the equations for calculating
the resolving power of a transmission grating immersed between two prisms.
Figure:
Diagram of a prism model for an immersed transmission grating.
In Littrow configuration, with both prism angles equal to 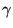 ,
the
resolving power is approximately proportional to
,
the
resolving power is approximately proportional to
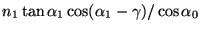 .
.
![\includegraphics[width=\textwidth]{prism-mod.eps}](img7.gif) |
Figure 1 shows the prism model that we are using with the
appropriate angles defined. Light passing through the prism and the immersed
grating, with a total beam deviation of
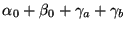 ,
obeys the following equations:
,
obeys the following equations:
The resolution can be determined by solving
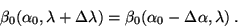 |
(4) |
Here, the output angle is regarded as a function of the input angle and the
wavelength. This expression represents the condition that incrementing the
wavelength by
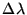 shifts the output image by the same amount as
does the change in the incidence angle across the slit width.
shifts the output image by the same amount as
does the change in the incidence angle across the slit width.
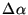 is the angular size of the slit in the collimated beam and is given by
is the angular size of the slit in the collimated beam and is given by
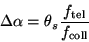 |
(5) |
where 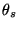 is the angular size of the slit on the sky, and
is the angular size of the slit on the sky, and
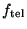 and
and
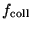 are the effective focal lengths of the telescope and
collimator. If n1 and n0 are independent of wavelength (i.e., ignoring
differential refraction), then Eqn. 4 can be solved
analytically to give a resolving power of
are the effective focal lengths of the telescope and
collimator. If n1 and n0 are independent of wavelength (i.e., ignoring
differential refraction), then Eqn. 4 can be solved
analytically to give a resolving power of
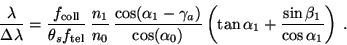 |
(6) |
Note that, with
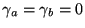 ,
this reduces to the well known
equation for the resolution of an unimmersed grating:
,
this reduces to the well known
equation for the resolution of an unimmersed grating:
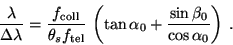 |
(7) |
To include the dispersive effects of glass (n1 varying with 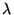 ),
Eqn. 4 can be solved numerically. Differential
refraction marginally increases the resolving power for typical VPH grism
designs.
In Littrow configuration,
),
Eqn. 4 can be solved numerically. Differential
refraction marginally increases the resolving power for typical VPH grism
designs.
In Littrow configuration,
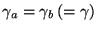 and
and
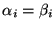 ,
with a total beam deviation of
,
with a total beam deviation of
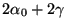 ,
the
resolving power (n0 and n1 constant) is given by
,
the
resolving power (n0 and n1 constant) is given by
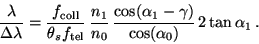 |
(8) |
The usefulness of Littrow configuration is three fold: (i) VPH unslanted
fringes can be used (slanted fringes may curve during DCG processing); (ii)
the beam size remains about the same, which keeps the camera optics smaller
and simpler; and (iii) the angular size of the slit remains nearly the same.
With unslanted fringes, the important Bragg angle is given by
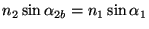 .
Figure 2 shows
resolving powers at Littrow versus total beam deviation with the Bragg angle
annotated. Note that for a given grating (fixed diffraction order, wavelength
and lines
.
Figure 2 shows
resolving powers at Littrow versus total beam deviation with the Bragg angle
annotated. Note that for a given grating (fixed diffraction order, wavelength
and lines
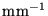 ), prisms typically reduce resolving power, but
for a given total beam deviation, prisms typically increase resolving
power .
), prisms typically reduce resolving power, but
for a given total beam deviation, prisms typically increase resolving
power .
Figure:
Resolving powers of VPH transmission gratings versus total
beam deviation. The top line represents a grating immersed between two
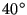 prisms (with n1=1.5), the dashed line between two
prisms (with n1=1.5), the dashed line between two
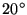 prisms and the lower line represents a grating with no prisms attached. The
crosses are set at
prisms and the lower line represents a grating with no prisms attached. The
crosses are set at
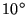 intervals in Bragg angle (with n2=1.3). The
resolving powers are normalized to unity for the zero deviation
intervals in Bragg angle (with n2=1.3). The
resolving powers are normalized to unity for the zero deviation
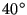 prism model. See Fig. 1 for the prism model. Note that
the dispersion caused by differential refraction is not included.
prism model. See Fig. 1 for the prism model. Note that
the dispersion caused by differential refraction is not included.
![\includegraphics[width=\textwidth]{prism-res.ps}](img34.gif) |



Next: Bibliography
Ivan Baldry
2004-11-19
![\includegraphics[width=\textwidth]{prism-mod.eps}](img7.gif)
![\includegraphics[width=\textwidth]{prism-mod.eps}](img7.gif)
![\includegraphics[width=\textwidth]{prism-res.ps}](img34.gif)