A second-order Hubble Law

Ivan K. Baldry
Astrophysics Research Institute, Liverpool John Moores University
IC2, Liverpool Science Park, 146 Brownlow Hill, Liverpool, L3 5RF, UK

Date: publication date 2021

The Hubble law is often stated such that the recession velocity is equal to the Hubble constant times the distance, with the most common approximation for velocity given by $c z$. However, a more useful expression for velocity (e.g. Emsellem et al., 2019; Cappellari, 2017) is given by

$$v = c \ln(1+z) \: .$$ (1)

This is more accurate for pure line-of-sight velocity and means that the peculiar velocity and cosmological terms, and frame corrections, are additive (Baldry, 2018). A common misconception is to assume $c z$ terms are additive. Coupled with different distance definitions, there are thus many versions of a Hubble law.

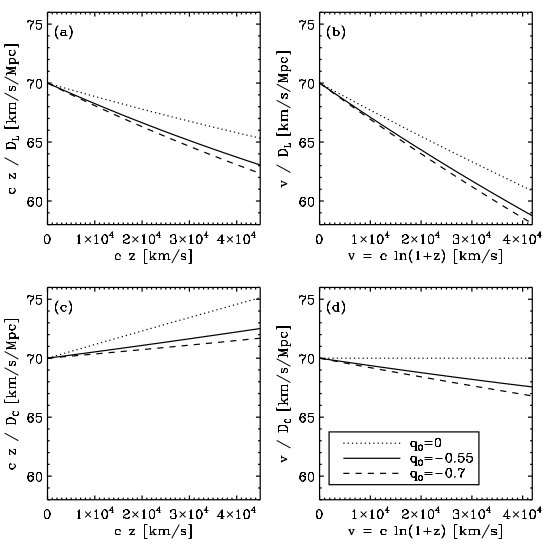
Figure 1: Different views of the Hubble law. The relations shown are for: a coasting cosmological model ($q_0=0$), a flat $\Omega _{m,0}=0.3$ model ($q_0=-0.55$), and a flat $\Omega _{m,0}=0.2$ model ($q_0=-0.7$).

Figure 1 shows four different views of the Hubble law using these approximations for velocity with luminosity distance ($D_L$) and line-of-sight comoving distance ($D_C$). For each version, curves are shown for three model cosmologies, all with flat geometry and with $H_{0}=70$ km s$^{-1}$ Mpc$^{-1}$. Two are $\Lambda$CDM models, for which the deceleration parameter $q = {\Omega_m}/{2} - \Omega_{\Lambda}$, while the other is a `coasting' model with $w=-1/3$. Notably, none of these versions of the Hubble law are accurate except in the case of (d) $v = c \ln(1+z) = H_{0} \, D_C$ for the coasting model (Sutherland & Rothnie, 2015). Note this exact law also is valid for a non-flat coasting model such as an empty universe [though in this case, $D_L \neq (1+z) D_C$]. Below we show a derivation of a second-order Hubble law that is natural in this view with a transparent dependence on $q_0$.

For demonstration purposes, we consider a flat universe with a single type of fluid with equation of state $w$ such that:

$$q \:=\: \frac{1+3w}{2} E(z) \:=\: (1+z)^{q+1}$$ (2)

The comoving distance is then given by

$$D_{\rm C} \:=\: \frac{c}{H_0} \int_0^z \frac{{\rm d}z}{E(z)} \:=\: \frac{c}{H_0} \int_0^z \frac{{\rm d}z}{(1+z)^{q+1}}$$ (3)

Using the logarithmic shift $\zeta = \ln (1+z)$, this becomes

$$D_{\rm C} \:=\: \frac{c}{H_0} \int_0^\zeta \frac{(1+z)}{E(z)} {\rm d}\zeta \:=\: \frac{c}{H_0} \int_0^\zeta e^{-q \zeta} \, {\rm d}\zeta$$ (4)

and after integrating ($q \neq 0$),

$$D_{\rm C}\:=\: \frac{c}{H_0} \left[ \frac{1}{q} (1 - e^{-q \zeta} ) \right]$$ (5)

For a non-constant $q$, the above result is valid only over a small change in $\zeta$. For small $\zeta = v/c$, using a second-order Taylor series expansion, we obtain a second-order Hubble law:

$$D_{\rm C} \:\simeq\: \frac{c}{H_0} \, \zeta \, \left( 1 - \frac{q_0 \zeta}{2} \right) \:=\: \frac{v}{H_0} \left( 1 - \frac{q_0 v}{2 c} \right)$$ (6)

This form tends to the exact law with $q_0 \rightarrow 0$, and the right-hand term [ $1 - (q_0/2)(v/c)$] represents an average of $(1+z)/E(z)$ assuming constant acceleration (c.f. the quadratic fitting function given by Sutherland & Rothnie (2015) for improved precision).

For $\Lambda$CDM cosmologies, the approximation is accurate to within 0.1% at $z \lesssim 0.1$. Note that regardless of the accuracy of the Hubble law, $v$ accurately represents the integral of the velocity differences along the line-of-sight, precisely in the case of fundamental observers. This is evident from the additive nature of terms in $\zeta$ or $v$ (Baldry, 2018).

   

This article was published as an appendix of a paper on `The effects of peculiar velocities in SN Ia environments on the local H0 measurement' by Sedgwick, Collins, Baldry & James (2021).