Cosmological scalefactor

At a team meeting, I once presented a slide jokingly noting that “z is an abomination, it is neither multiplicative, additive or a shift”. Of course, redshift's saving grace is that a human's computational ability is sufficient to convert $z$ to the inverse scalefactor, add unity and you get $1 + z_{\rm cos} = a^{-1}$, where $a$ is the cosmological scalefactor with the common convention that the present-day value $a_0=1$.

Using the logarithmic shift $\zeta$, the relationship is evidently $\zeta_{\rm cos} = \ln a^{-1}$. Spacing in logarithm of the scalefactor has desirable properties when considering galaxy populations or cosmology (Table 1). Figure 2 shows the separation in line-of-sight comoving distance ($D_{\rm C}$) versus redshift and zeta for two different cosmologies. The black lines show

$$S_z \: = \: 0.01 \frac{{\rm d}D_{\rm C}}{{\rm d}z} S_{\zeta} \: = \: 0.01 \frac{{\rm d}D_{\rm C}}{{\rm d}\zeta}$$ (14)

in each plot. These are inversely proportional to $\dot{a}/a$ (e.g. Hogg 1999) and $\dot{a}$, respectively. Notably $S_{\zeta}$ varies less, particular at $\zeta < 1$. This is a desirable property since large-scale structure is evaluated using comoving distances. Spacing in $\zeta$ corresponds to constant velocity and approximately constant comoving distance.

Figure 2: Comparison between spacing in redshift and zeta. The black lines show the comoving separation per 0.01 in $z$ (left) and $\zeta$ (right) (Eq. 14). The solid lines represents the `737 cosmology' ($h=0.7$, $\Omega _{\rm m}=0.3$, $\Omega _{\Lambda }=0.7$) while the dashed lines represent an Einstein-de-Sitter cosmology ($h=0.37$ arbitrary, $\Omega _{\rm m}=1$). The dotted lines show the points at which the universe was one half, one quarter, etc., of its present-day age for the 737 cosmology.

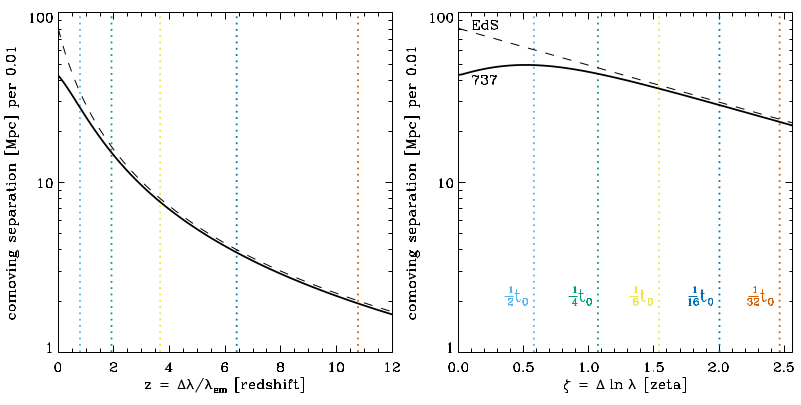The turnover in $S_{\zeta}$ demonstrates the onset of dark energy dominating the dynamics for the `737 cosmology'. This is evident even without the comparison to the Einstein-de-Sitter (EdS) cosmology because for a non-accelerating universe ( $\ddot{a}=0$), $S_{\zeta}$ is constant. For the EdS model, $S_z \propto a^{3/2}$ and $S_{\zeta} \propto a^{1/2}$ so that

$$\ln S_{\zeta} = -\frac{1}{2} \zeta + \ln (0.01\,c/H_0)$$ (15)

which explains why the dashed line is straight in the right plot of Figure 2. See, for example, fig. 2 of Aubourg et al. (2015) for related plots [using $\dot{a}$ and $\ln (1+z)$] comparing different models of dark energy, and Sutherland & Rothnie (2015) who advocated changing the redshift variable to $\ln (1+z)$ in analysis of luminosity distance residuals.

Also shown in Figure 2, with vertical lines, are the points at which the universe halves its age (737 cosmology), with increasing $z$ and $\zeta$. For $z$, the last half of cosmic time covers only a small fraction of the plot ($z<0.8$), whereas for $\zeta$, the spacing is approximately logarithmic in time. For an EdS model, it would be equally spaced in $\ln t$ because $a \propto t^{2/3}$. For the 737 cosmology, an increase in $\zeta$ of $\sim 0.5$ corresponds to halving the age of the universe across the epochs shown. A generic plot related to galaxy evolution shows the cosmic star-formation rate (SFR) density, logarithmically scaled, versus $z$ but often scaled linearly in $\ln (1+z)$ (Madau & Dickinson, 2014; Hopkins & Beacom, 2006). This a recognition of the aesthetic of $\ln(a)$ separation.

Table 1: zeta-redshift-scalefactor lookup

$\zeta$	$z$	$a$	note
0.1	0.105	0.905	$\sim$ present-day galaxy properties
0.5	0.649	0.607	$\sim$ transition to cosmic acceleration
1.0	1.72	0.368	$\sim$ peak of cosmic SFR density
1.5	3.48	0.223
2.0	6.39	0.135	$\sim$ end of reionization
2.5	11.2	0.0821
3.0	19.1	0.0498	$\sim$ first stars
7.0	1096	0.000912	$\sim$ matter-radiation decoupling